- Details
-
Published: Tuesday, 03 June 2025 01:29
-
Hits: 492
Calculus:
We'll start with limits and then move to differentials and integrals.
Nice cheat sheet showing all imp Calculus formulas => https://math.colorado.edu/math2300/resources/calc1/lamar/Calculus_Cheat_Sheet_All.pdf
Limits:
Limits are one of the easiest to master. They form the basis of calculus. When we say limit, we are trying to find the value of a function, as it approaches a particular value of a variable.
ex; Y= 2*x+5. This is a straight line, and when I say what is the value of Y at x=3, it's 2*3+5=11. No if I say, what's valve of Y as x approaches 3 from left side of graph (denoted as -> 3-), or from right side of graph (denoted as -> 3+), it's still 11. So, most of the cases limit is as simple just substituting the value.
In some, the exact value of the Func doesn't exist at that point, but in this case, limit may still exist, since Limit says it approaches that value, but is never exactly that value.
ex: Y = (x^2-4)/(x-2). Here at x=2, the function is 0/0 which is undefined. However, we can write it as Y=(x-2)(x+2)/(x-2). If x≠2, then we can cancel out (x-2) from top and bottom, and func Y=(x+2). Now as x->2 (from left or right), the value is 4. However, at exactly x=2, the value doesn't exist (you mark it as a open dot instead of a filled in dot).
When evaluating limits, Func which yield values as 0/0, ∞/∞, 0*∞ are all undefined, and hence you have to either cancel out some term, or rewrite the expression so that it can be evaluated to a known value on substitution (and NOT yield undefined values). Most of the complicated function limits are evaluated by expanding the complex function as Taylor series (i.e as polynomial function). Then something usually cancels out leading to a lmit value.
Some well known limits are:
- Lt x->0 (sin(x))/x = 1 (write sin(x) as Taylor series and cancel out x from numerator and denominator). It's 0/0, but evaluates to 1 in limiting case.
- Lt x->0 (1-cos(x))/x = 0 (expand using Taylor series). It's 0/0, but evaluates to 0 in limiting case (unlike sin case above which evaluates to 1).
- Lt x->∞ (1+1/x)^x = e. Here inside term goes to 0 while exponent term goes to ∞, so hard to see it can approach a particular value as e.
- More limits => https://planetmath.org/ListOfCommonLimits
Differentiation (Derivatives):
Differentiation follows from limits. A derivative of a function is the slope of a function at every point of the function. The slope at a point is defined as a line that touches the function at only 1 point. This slope itself may be another function, and it's denoted as f´(x) (i.e f with a prime on top).
Avg slope of a function b/w any 2 points x1 and x2 is = [f(x2)-f(x1)] / (x2-x1). Now if we start getting x2 closer to x1, then avg slope we get is for a narrower section of the function. If we make x2 infinitesimally close to x1, then, in the limiting case, we get the slope of the function at the point x1.
Let's rewrite x2 as x2=x1+Δx, then slope = [f(x1+Δx) - f(x)] / Δx
So, f´(x) = Lt Δx->0 [f(x+Δx) - f(x)] / Δx => The eqn we get for derivative is the function that shows the slope of f(x) at any point x.
ex: f(x)=x^2, find f´(x). Here we find derivative using the defn above.
f´(x) = Lt Δx->0 [f(x+Δx) - f(x)] / Δx = Lt Δx->0 [(x+Δx)^2 - x^2] / Δx = Lt Δx->0 [2.x.Δx + Δx^2]/Δx = Lt Δx->0 [Δx(2.x+Δx)] / Δx = Lt Δx->0 2.x+Δx = 2.x
So, slope of function x^2 is 2.x at any point x. We can verify this by drawing slopes at x=1, x=2, x=4, etc and confirm that the slope is indeed 2, 4, 8, which is 2.x !!
Similarly derivatives can be found for many common functions. In most cases, we have to do a Taylor series expansion to cancel out Δx in both numerator and denominator.
f(x)=sin(x). To find f´(x), we expand sin(x) as Taylor series,, cancel out Δx, and the series left is cos(x). So, f´(x) = cos(x)
If f(x)=cos(x), then f'(x) = -sin(x)
Cheat sheet => https://tutorial.math.lamar.edu/pdf/calculus_cheat_sheet_derivatives.pdf
Derivative Rules:
- Constant Multiple Rule: d/dx[k*f(x)] = k* d/dx(f(x)), where k is a constant.
- Power rule: d/dx(x^n) = n*x^(n-1). Most widely used to differentiate polynomials. Any continuous function can be written as a polynomial, so individual terms of the polynomial can be differentiated using this formula. If we keep on differentiating poly of x^n n times, then it will keep reducing the power of poly func by 1 each time, and ultimately the result would be 0.
- Sum/Difference Rule: d/dx [f(x) + g(x)] dx = d/dx[f(x)] + d/dx[g(x)] (instead of +, we can have - too)
- Product rule: d/dx [f(x).g(x)] = g(x).d/dx(f(x) + f(x).d/dx(g(x) => basically you differentiate each function separately and multiply it with the undifferentiated func.
- Quotient Rule: d/dx [f(x)/g(x)] = g(x).d/dx(f(x) - f(x).d/dx(g(x) / [g(x)]^2. This can be derived from product rule as g(x) can be replaced with 1/g(x). Then d/dx(1/g(x)) = -1/[g(x)]^2 * d/dx(g(x)) and we get the quotient rule.
- Chain Rule: Written in 2 forms:
- d/dx [f(g(x))] = d/d(g(x) [f(g(x))] * d/dx(g(x)) => NOTE: the 1st derivative is wrt g(x) and NOT x. You may substitute g(x) with var "u". That is the form that the 2nd form of chain rule is written in as shown below.
- dy/dx = dy/du * du/dx where y may be written as a func of var u.
Some common derivatives:
Link for common derivatives and rules => https://www.mathsisfun.com/calculus/derivatives-rules.html
- d/dx(e^x) = e^x (drive from defn of derivative, and then using series expansion of e^x).
- d/dx (a^x) = ln(a). a^x. We can derive this from differentiation of e^x. a^x can be rewritten as e^(x ln(a)). This is because if we take natural log of both sides, then ln(a^x) = ln (e^(x ln(a)) => x (ln a) = x (ln a), so both sides become equal. Now d/dx(a^x) = d/dx(e^x(ln a) = e^(x(ln a)) . d/dx(x * ln(a)) = ln (a). e^(x(ln a) = ln(a). a^x.
- d/dx(ln x) = 1/x . Since ln (x) is inverse fn of e^x, we can use above derivative of e^x to find this one. Let y=ln(x) => x=e^y, => d/dx(x) = d/dx(e^y) => 1 = d/dy(e^y).dy/dx => 1=e^y.dy/dx => dy/dx = 1/e^y = 1/x .
- NOTE: ln (x) is only defined for x>0. This will be important in integral (discussed below) as If we want to have ∫ 1/x = ln(x) only for x>0. If x<0 in limits, then we can only do integral only if we take mod x, i.e ln |x|. So ∫ 1/x = ln(|x|) if we want to be exact. This ensures that just as 1/x graph exists in 1st and 3rd quadrant, ln(x) exists in all 4 quadrants for all values of x.
- d/dx(logax) = d/dx(ln(x)/ln(a)) = 1/(x.ln(a)).
- d/dx(tan(x)) = d/dx((sin(x)/cos(x)). Using quotient rule, we get f'(x)= sec2(x)=1/cos2(x)
- d/dx(cot(x)) = d/dx((cos(x)/sin(x)). Using quotient rule, we get f'(x)= -cosec2(x) = -1/sin2(x). Or other way is by using d/dx(1/f(x)) where f(x)=tan(x). So, d/dx(1/tan(x)) = -1/tan2(x).d/dx(tan(x)) = -1/tan2(x).(1/cos2(x)) = -1/sin2(x)
Tricky differentiation using above rules:
- ex: d/dx(x^x). Take y=x^x => ln(y)=xln(x) => d/dx(ln(y)) = d/dx(xln(x)) => 1/y*dy/dx=ln(x) + 1 => dy/dx=y[1+ln(x)] => d/dx(x^x) = x^x * [1+ln(x)]
Derivative of inverse functions:
If we have f(x) and it's inverse g(x)=f-1(x), then if slope of f(x) = m at pt (x1,y1), then slope of g(x) will always be 1/m. Reason being that inverse function is just y replaced by x (and x replaced by y). So if original func f(x) had slope m=Δy/Δx, then it's inverse func g(x) will have slope Δx/Δy (as x and y are interchanged for inverse func), which is = 1/m. So, the g´(x) = 1/f´(x). The only point to watch out is that if the slope of original func f(x) was at point (x1,y1), then the inverted slope is at point (y1,x1) as the x,y coordinates get interchanged. So if f(x) slope is m at (b,a), then g(x) slope will be 1/m at (a,b). => a=f(b) => b=f-1(a)
g´(x=a) = 1/f´(x=b) => g´(x=a) = 1/f´(x=b) => g´(x=a) = 1/f´(g(x=a))
ex: f(x)=x^2, then g(x)=f-1(x)=√x
f´(x)=2x, g´(x)=1/(2x), At x=3, f´(x)=2x=6 (at coord (3,9)), so g´(x)=1/(2x) = 1/6 at coord (9,3). NOTE: the coordinates chaged. If we want to find g´(x=3) (i.e coord (3,√3)), then we need to find f´(x=√3) = 2√3 => g´(x=3) = 1(2√3)
We can also use above formula directly: g´(x=a) = 1/f´(g(x=a)) => Since g(x=3) = √3, g´(x=3) = 1/2x @x=√3 = 1(2√3), which is same as what we obtained above.
Maxima/Minima:
Derivatives can be used to find maxima and minima if functions. This is one of the most used application of derivatives in real life.
Following defn used to describe shapes of func when dealing with max/min:
- Convex func: (aka Concave upward or convex downward): Any func whose slope increases is convex or concave up (like a rice bowl kept on table), i.e slope goes from -ve to 0 to +ve or any part where slope is increasing.
- Concave func (aka concave downward or convex upward): Any func whose slope decreases is concave or convex up (like a rice bowl kept upside down on table), i.e slope goes from +ve to 0 to -ve or any part where slope is decreasing.
- Infection point: This is the point where the func changes from convex to concave or vice versa.
A continuous and smooth function (most of the real functions are smooth, an exception is absolute value func) will have it's slope=0 at maxima and minima. These are local max/min, as many of these local max/min may exist. There's no way known to find the absolute max/min of any func. Over a limited domain of x values (i.e x goes from x1 to x2), we can determine absolute max/min by looking at all points where slope is 0, undefined or at end points. Whether the point is maxima or minima is determined by 2nd derivative.
- 1st derivative: Given f(x), find first derivative f'(x). If f'(x) =0 at x=x1, it's either a maxima, a minima or a infection point. An infection point is a point where slope is 0, but instead of reversing direction (i.e slope), it keeps on moving in same direction.
- 2nd derivative: Now find 2nd derivative f''(x) at x=x1. Depending on 2nd derivative sign, we can determine whether it's max or min
- Maxima: If f''(x1) < 0, then x1 is a point of local maxima. This is because, at maxima, it's concave, so slope of this func goes from +ve to -ve (decreasing). Then, derivative of this slope (i.e f''(x)) will be -ve. If you don't want to check for 2nd derivative, then you can also check sign of first derivative, f'(x). If f'(x) changes sign from +ve to -ve when going thru x1, then it's a maxima.
- Minima: If f''(x1) > 0, then x1 is a point of local minima. This is because, at minima, it's convex, so slope of this func goes from -ve to +ve (increasing). Then, derivative of this slope (i.e f''(x)) will be +ve. If you don't want to check for 2nd derivative, then you can also check sign of first derivative, f'(x). If f'(x) changes sign from -ve to +ve when going thru x1, then it's a minima.
- Infection point: Here, func changes from convex to concave or vice versa, implying f''(x) changes sign from +ve to -ve or vice versa. Basically f''(x)=0 at point of infection (as sign change can only happen when it passes thru 0). At infection point, slope of the original func, f(x), may or may not be 0 (i.e f'(x)=0 or f'(x)≠0).
- If f'x(0)=0 and f''(x)=0, then func continues going in same dirn after hitting a flat portion. No max or min exists, though slope of f(x) does go to 0
- If f'x(0)≠0 and f''(x)=0, then func is changing shape from convex to concave or vice versa. No max or min exists as slope of f(x) never goes to 0
Integration (Integral):
Integration is inverse of differentiation. Integral is the inverse function of derivative. We denote it as ∫ f(x). Given function f(x), if F´(x) = f(x), then ∫ f(x) = F(x). F(x) (denoted with capital F) is the inverse func of f(x). See Inverse function in other sections.
F(x) -> differentiate -> f(x). F´(x) = f(x),
F(x) <- integrate <- f(x). F(x) = ∫ f(x).
Integration was originally developed as "finding area under curve". Later Barlow and Toricelli in 17th century found hints of connection b/w differentiation and integral. Barrow provided the 1st proof of "fundamental Thm of Calculus". Later Newton and Leibniz did more advanced work on calculus, where integral was found to be inverse function of differentiation, which made it easy to solve integral
But why is integration area under a curve? Let's say A(x) is some function of f(x). At x=x1, A(x) is A(x1). Now, if we take incremental "dx" at x=x1, and compute f(x).dx, then f(x).dx gives area of the incremental rectangle formed. So, incremental increase in area is f(x).dx. So, A(x) must be the area of the function, as incremental area dA(x)=f(x).dx => dA(x)/dx = f(x). Or A(x) = ∫ f(x).dx
This vid shows it formally by using MVT => https://www.youtube.com/watch?v=U3u0PF7n-xg
Integration is usually taught as avg value of a continuous func. To make it easier, we divide f(x) into N discrete sections and then find avg value.
Then avg = [∑f(x) ] / N, where summation is over N points, and each point is spaced apart by dx, so no. of points N = (b-a)/dx. So, area = Avg height of f(x) * base = [∑f(x) ] / (b-a) * dx * (b-a) = [∑f(x) ] * dx where a,b are endpoints on x axis
Now if we start taking limit dx->0, then avg value of this func approaches closer to it's real value. So, Area = Limit dx->0 [∑f(x) ] * dx = b
a∫ f(x).dx
Fundamental Thm of Calculus: b
a∫ f(x).dx = F(b) - F(a) where F´(x) = f(x). There are 2 parts of this Thm, but they are almost same, I'm writing both parts as one (strictly there are 2 parts). What's insane is that the area of the whole curve can be found by just looking at the values of antiderivative at the endpoints o the curve !! We'll see why that happens below.
Essence of Calculus explaining Integration as area under curve => https://www.3blue1brown.com/lessons/integration
We learn integration as the area under the curve. However, the function that we get via integration F(x) is actually the inverse function of f(x), i.e F´(x) = f(x). But differentiation gives the slope, while it's inverse func gives the area. How is the slope and area related? This fundamental question is explained nicely here => https://www.3blue1brown.com/lessons/area-and-slope
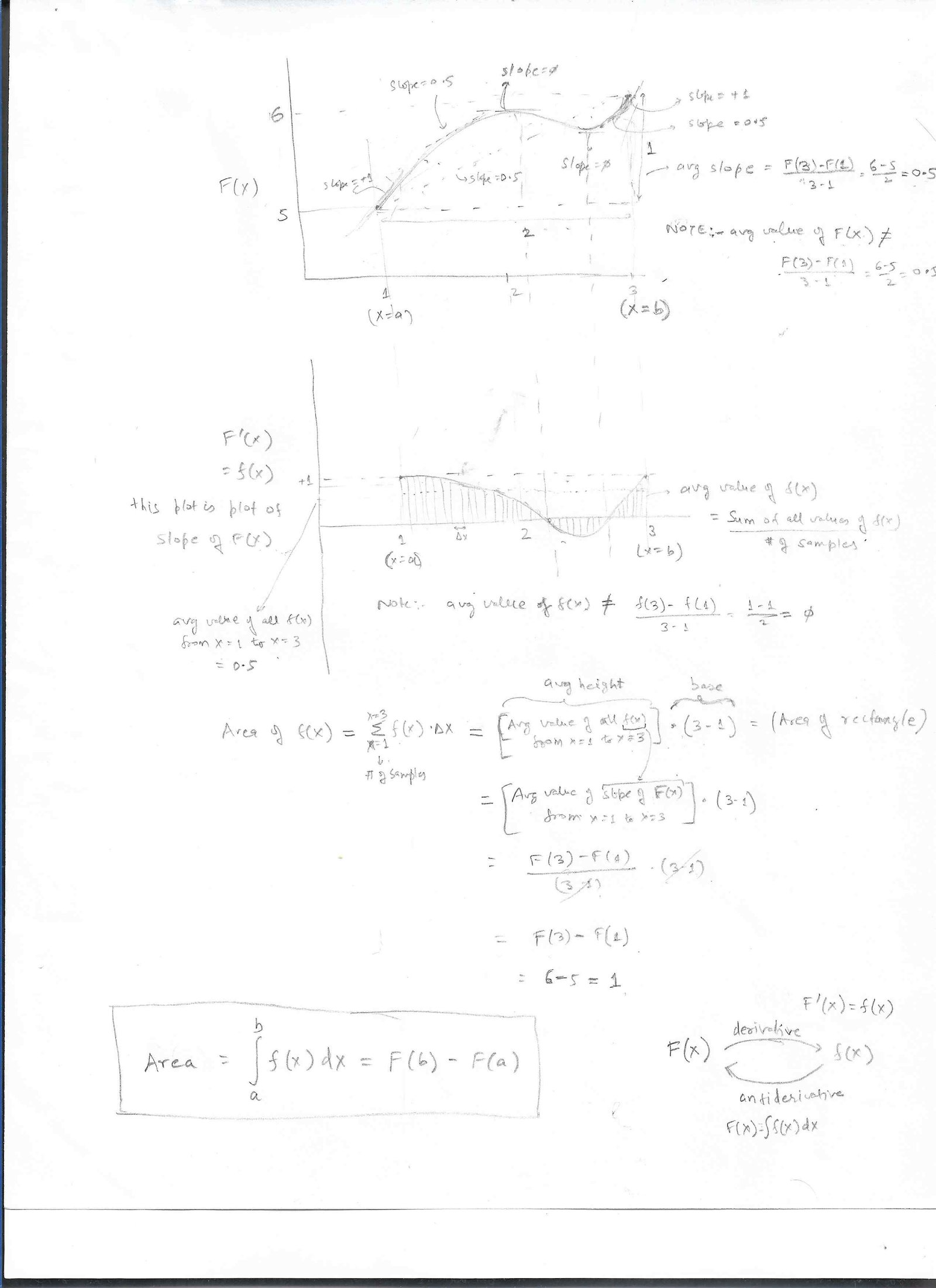
To see this relationship, 2 key points to observe:
- Avg slope for any func can be calculated by just looking at End Points: If you were given a bunch of numbers in any order, would you be able to calculate it's avg just by looking at 1st and last number? Answer is => NO. You won't be as the avg is decided by all the numbers. Now consider continuous plot of such numbers. Again, it's the same thing => you won't be able to calculate the avg of this continuous func, just by looking at the 2 endpoints of the curve. But now, let's say, I calculate the slope of this function, and plot this new function which is the slope of our original function at every point of the graph. Can I calculate the avg of this slope function, by just looking a the 2 endpoints? Surprisingly, you can now. Why does this happen. Because, with slope, if the slope goes up a certain magnitude above the avg, the slope has to come down the same magnitude below the avg, to give us the avg. It also follows from Mean Value Thm and from intuition. So, the jist is => The avg slope (rate of change of Y wrt X) of any function could be found by just looking at the 2 endpoints.
- Area of a function: it can be calc as avg height of func multiplied by the width of the base. The avg slope of any func as seen above = [F(b)-F(a)]/(b-a), where a,b are endpoints on x axis. If we plot the slope function (i.e a function f(x) that is the slope of F(x) for all points on x axis), then the area of f(x) will be = Avg height of f(x) * base. But avg height of f(x) = avg slope of F(x) (as f(x) is slope func of F(x)). Since avg slope of F(x) = [F(b)-F(a)]/(b-a), that's the avg height of f(x). So, area of f(x) = avg height of f(x) * base = [F(b)-F(a)]/(b-a) * (b-a) = [F(b)-F(a), which proves the theorem.
Diagram showing proof of Fundamenal Thm of Calculus
Finding area of a curve:
As we saw above, We use this formula for area under a curve from x axis (Y=0) to the function f(x): Area = b
a∫ f(x).dx = b
a∫ y.dx (since f(x)=y). Other way to find area is to rotate the paper 90 degrees anticlockwise and then integrate with dy, i.e Area = f(b)
f(a)∫ x.dy Here limits a and b change to f(a) and f(b), since we are integrating along Y-axis. This gives the area of the remaining portion of the rectangle bounded by a, b, f(a), f(b). If we add up the 2 area, we should get the area of the rectangle minus the smaller rectangle = [b*f(b)) - a*f(a)].
ex: y=x^2. Area from x=1 to x=3 is b=3
a=1∫ y.dx = b=3
a=1∫ x^2.dx = [x^3/3] from x=1 to x=3 => 1/3[3^3-1] = 26/3.
Now we take area along y axis. Then x=√y. Limits are y=3^2=9, 1^2=1. So, area from y=1 to y=9 is b=9
a=1∫ x.dy = b=9
a=1∫ √y dy = 2/3* [y^3/2] from y=1 to y=9 => 2/3[9^3/2-1] = (26*2)/3.
The area of the rectangle formed is (3*9)-(1*1) = 27-1 = 26, which is the sum of 26/3+26*2/3=26.
NOTE: Area of the figure under the X-axis is calculated as -ve while area above the x-axis is calc as +ve (automatically happens the way we integrate). If we want to find the absolute area, then we have to find the area of the regions separately and then add the absolute values of the 2 area.
Finding arc length of a curve:
To find the arc length, we use pythagoras thm in calculus.
Any length Δl2 = Δx2 + Δy2 => Total length of arc from x=a to x=b is [∑Δl ] = [∑√ ( Δx2 + Δy2) ] = ∑[√ ( 1 + Δy2/Δx2 ) * Δx] = b
a∫ √ ( 1 + dy2/dx2 ) ] * dx (by converting to integral) = b
a∫ √ ( 1 + f’(x)2 ) dx
2dl/dx = 2 + 2dy/dx (differentiating both sides wrt dx) => dl/dx = 1 + f’(x)
As we saw above, We use this formula for area under a curve from x axis (Y=0) to the function f(x): Area = b
a∫ f(x).dx = b
a∫ y.dx (since f(x)=y). Other way to find area is to rotate the paper 90 degrees anticlockwise and then integrate with dy, i.e Area = f(b)
f(a)∫ x.dy Here limits a and b change
Finding Volume under a curve:
Generally for finding volume, surface area, etc, we need to use 2D calculus (involving both var dx and dy). But many times, these 3D figures are symmetric, and we are able to generate the 3D figures from the 2D figure by making concentric circles, etc. Then we can find volume or surace area by just using single variable, dx.
ex: Find volume of sphere: Here we take a circle at distance x from the center of sphere, and cut out this circle of thickness dx. Then all these slices of circles added up gives the volume of sphere. x^2+y^2=R^2. V = 2* b=R
a=0∫ Π * y^2.dx = 2*Π* b=R
a=0∫ [R^2-x^2]dx = 4/3*Π*R^3
Integral formulas:
Cheat sheet => https://tutorial.math.lamar.edu/pdf/Calculus_Cheat_Sheet_Integrals.pdf
As explained above, integrals are just inverse function of differentials. There are 2 types of integrals:
- Definite integrals: When we provide limits on the integral (i.e finding integral for a function with limits of a->b. b
a∫ f(x).dx ), then it's called a definite integral. The result will be a constant (with no "x" variable in it). This represents the area under the curve.
- Indefinite integrals: When we don't provide limits (i.e ∫ f(x).dx), then it's called an indefinite integral. The result will be a function of x, which is actually the inverse function (with a "x" variable in it). This represents the general solution, and so we need to add a constant C, i.e ∫ f(x).dx) = F(x) + C. We add a constant C, as differential of constant gives 0, so any constant can be added to any function, and differential will still be the same.
Integration Rules:
- Constant Multiple Rule: ∫ k * f(x) dx = k * ∫ f(x) dx + C, where k is a constant. Constant C is added for all indefinite integrals, even if we don't write it everytime.
- Power rule: ∫ x^n dx = (x^(n+1))/ (n+1) + C (C is a constant). It can be easily seen to be true as d/dx(x^n) = n*x^(n-1). Any func that can be broken down into polynomial with individual terms should use this formula to get integral
- Sum/Difference Rule: ∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx.
- Integration by Parts (or partial integration = PI): Written in 2 forms:
- ∫ udv = u * v – ∫ v du, where u and v are differentiable functions. Can be proved from differentiation: d/dx(uv) = v.du/dx + u.dv/dx => d(uv) = vdu + udv => integrating both sides, we get ∫d(uv) = ∫udv + ∫vdu => uv = ∫udv + ∫vdu => ∫udv = uv-∫vdu. For definite integral, this formula becomes b
a∫ udv = uv| b
a - b
a∫ vdu. If we write u=f(x) and v=g(x), then above form can be rewritten in terms of x as => ∫f.g´dx = f.g – ∫g.f´dx (exactly same form, just written differently)
- ∫ [f(x).g(x)]dx = f(x)∫g(x)dx – ∫f'(x){∫g(x)dx}dx where f(x), g(x) are any two functions. This can be directly seen by choosing u=f(x) and v=∫g(x)dx (i.e dv/dx=g(x) => dv=g(x)dx). Now substituting u,v in formula above, we get ∫ udv = u * v – ∫ v du => ∫ [f(x).g(x)]dx = f(x)∫g(x)dx – ∫ { [ ∫g(x)dx] f´(x)} dx , which is the same form as what we wanted to prove. NOTE: We have f'(x) (derivative of f(x)) in last term and NOT f(x)).
- This is a very imp formula used to solve integrals that can't be solved by any other method. There are rules on how to choose u and dv (i.e f(x) and g(x)). g(x) should be chosen such that you can integrate it easily. Remaining function is f(x), and derivative of this func f(x), which is f'(x) multiplied with G(x) (integrated function of g(x)) should also be integrable. This is tough to see for any arbitrary function. There's no hard rule on how to attack a function for PI, though some heuristics exist (shown below).
- ex: ∫ ln(x)dx => this can only be solved by PI. Choose u=ln(x), dv=dx. This will allow us to solve, as both u, v are easily solvable.
Some common integrals: (NOTE: integrals are just inverse function of differentials)
- ∫ e^x dx = e^x +C (C is a constant). It can be easily seen to be true as d/dx(e^x) = e^x.
- ∫ a^x dx = 1/ ln(a) * a^x as d/dx (a^x) = ln(a). a^x.
- ∫ 1/x dx = ln(|x|) as d/dx(ln x) = 1/x. We need to have absolute value of ln(x) as log is not defined for -ve number. If we have ∫1/(x.ln(a)), then 1/ln(a) being a constant, just gets taken out, and then ln(x)/ln(a) can be rewritten as loga(x)
- ∫ sin(x) dx = -cos(x), ∫ cos(x) dx = sin(x), ∫ tan(x) dx= ∫ sin(x)/cos(x) dx. choose u=cos(x) => du = -sin(x) => ∫ tan(x) dx = - ∫ (1/u)du = -ln|u| = -ln|cos(x)|
ex: ∫ 1/[(x+3)(x+2)] = ∫ [1/(x+2) - 1/(x+3)] = ln(|x+2| - ln(|x+3|)


