- Details
-
Published: Sunday, 15 September 2024 15:25
-
Hits: 933
Trignometry: Trignometry is a branch of Geometry that deals exclusively with triangles. You may wonder how come triangles have a whole branch of Mathematics dedicated to itself !! There are lots of things that's possible with triangles, and knowing triangles well forms the basis of Geometry.
We learned about drawing various triangles, finding angles of a triangles, and sides of a right angle triangle.
We can find all sides of a triangle given it's angles or vice versa. We need to know sine, cosine and tangent for that. We'll learn about right angle triangles and then move to other generic triangles.
Radians: So, far we learned that unit of angle is degrees. That is what our protractor also shows. One other unit of angle is radian. It's very widely used in scientific community, because many ratios cancel out nicely when using radian. 180 degrees is defined as π (pi=3.14) radians.
So 1 radian = 180/π degrees (approx 57.3 degrees). So, 1 radian of angle is an angle which is slightly less than 60 degrees.
Right angle Triangle:
For a right angle triangle with any one of the angles as Θ, we will have ratios of all 3 sides of triangle fixed, i.e if we make any other right angle triangle with this angle, that triangle will be similar to this triangle. Infact all such triangles will have same shape, they will just differ in the scaling. it makes sense to define the ratio of the sides for all right angled triangles for a given angle Θ on it's base.
Consider right angle triangle with sides a,b,c, where a=vertical side, b=base, c=hypotenuse, and angle Θ = angle b/w hypotenuse and base. Then we have six ratios that we can define between the 3 sides. Below we define those six ratios.
| sin(Θ) = a/c |
cosec(Θ) = 1/sin(Θ) = c/a (aka cosecant) |
| cos(Θ) = b/c |
sec(Θ) = 1/cos(Θ) = c/b (aka secant) => cos was already used up, so putting co again sounds weird cocosecant, so we stick with secant
|
| tan(Θ) = a/b |
cot(Θ) = 1/tan(Θ) = b/a (aka cotangent)
|
This is the definition for all 6 ratios. Sine, cosine and tangent are the ones most commonly used. There are tables that give values of sine, cosine and tangent for all values of angle Θ, from 0 degrees to 90 degrees. By looking at the table, we can figure out lengths or angles for any given triangle.
Few basics of terms above:
- All 6 of the ratios are periodic. Sin/cos are periodic with period of 2π (360 degrees), while tan has a period of π (180 degrees).
- Sin, cos are continuous while tan becomes discontinuous at any odd multiple of π/2 (90 degrees, 270 degrees, etc).
- Cosine is just a shifted version of Sine, where the Sine function is shifted to the left by 90 degrees to form cosine
I've put the most common theorems for these 6 defn, and their relationship at 90, 180 and 360 degrees. It's easy to see these relations from the graph itself, or by using the formula defn of the triangle
Link => SIN/COS/TAN waveforms and equations
There are lot of theorems that can be derived for these 3 equations defined above. Lot more theorems are on link below.
- sin2(Θ) + cos2(Θ) = 1 (This can be proved by Pythagaros therem: (a/c)^2 + (b/c)^2 = (a^2+b^2)/c^2 = c^2/c^2 = 1). Most IMP formula, one you can't afford to forget.
- sin(Θ)/cos(Θ) = tan(Θ) (this can be proved by dividing sin and cos eqn above)
- sin(Θ) = cos(90-Θ). Similarly cosΘ) = sin(90-Θ). This can be proved by looking at the right triangle, and finding sine and cosine for the other angle which is (90-Θ). OR by noting that cosine is a 90 degree left shifted version of sine. See link above.
- 360+Θ is same angle as Θ, as 360 is one full rotation and comes back to starting line. So, is 360*n+Θ where n is an integer number. So, all 6 definitions above give same result for 360+Θ, i.e Sin(360*n+Θ)=Sin(Θ), where n is an integer (+ve or -ve)
- For all other angles between 0 to 360 clockwise (treated as +ve), above equations are defined depending on whether base and height are +ve or -ve. Hypotenuse is always taken as +ve. Height and base are taken as +ve or -ve depending on X and Y coordinate. Similarly for angles going anticlockwise, we treat those angles as -ve, and again define all equations above the same way. These equations are defined in this way, so that the same sin, cos, tan eqn will work in all quadrants.
- Many more formulas, and definition for angles > 90 degrees and < 0 degrees are in "unit circle" link below:
- One other imp formula is sum of angles: Sin(a+b) = Sin(a).Cos(b) + Cos(a).Sin(b). This can be used to derive Sin(a-b), Cos and tan sum/diff formula ver easily. This is harder to prove. One such proof is on Khan
- Academy => https://www.youtube.com/watch?v=R0EQg9vgbQw
- Cheat sheet for imp formulas => trig_cheat_sheet.pdf
So, we see that all 3 definitions above for sine, cosine and tangent are related to each other. If we know any one of the sine, cosine or tangent we can know the other 2 easily.
Unit Circle: We can also use a unit circle to learn these ratios. There is a unit circle that can be drawn. Then sin, cos, tan etc are just sides of that triangle inside and outside the circle.
Explained on this link: https://www.math10.com/en/algebra/sin-cos-tan-cot.html
Graphs of transformation of sin/cos functions:
So far we saw drawing Sin/Cos functions. However if we transform the eqn to be more generic like y = A*sin(B*x-C) + D, then sin/cos func is compressed/expanded + shifted up/down or left/right. It's similar to transformation of any function that we saw in earlier section. When f(x) gets transformed to A*f(B*x-C) + D, func shifts as well as get compressed/expanded. Exactly the same thing here with sin/cos. Below link explains well.
Link => https://math.libretexts.org/Courses/Rio_Hondo/Math_175%3A_Plane_Trigonometry/02%3A_Graphing_Trigonometric_Functions/2.04%3A_Transformations_Sine_and_Cosine_Functions
Inverse functions:
So far we saw drawing Sin/Cos functions. We have inverse functions for any given function.For ex, the inverse of square function is square root function, etc. For sin/cos/tan etc, the direct function converts from angle to a number. The inverse function gives us the angle back from that number. So, the domain of inverse function is from -1 to +1 and range is from -∞ to +∞. However since the forward function is periodic, the reverse func will give us multiple values of Θ for a given number. That violates the defn of func, which states that there can be a max of 1 Y value for a given x. To make it fit, we choose a range for inverse function so that none of the Y values are repeated. We define our inverse function only in this range. That's how officially inverse func for sin/cos/tan etc are defined.
Link => https://math.libretexts.org/Courses/Monroe_Community_College/MTH_165_College_Algebra_MTH_175_Precalculus/06%3A_Analytic_Trigonometry/6.01%3A_Inverse_Trigonometric_Functions
Drawing Right angled triangles:
It's important that kids draw right angled triangles. Then they should be able to figure out by themselves if they can draw a unique right angled triangle for a given angle. Following are cases where info is enough to draw a unique right angles triangle.
- Given Any 2 sides of right angles triangle => Pythogaros Thm gives us 3rd side, and all 3 sides (SSS) gives us unique triangle
- Given any one angle and one side of right angled triangle => Since 1 angle (X) is given, we can find out other angle (90-X). So, all 3 angles are known, and 1 side is known, so unique triangle can be drawn using ASA.
Ex: Draw a right angled triangle, with one angle=30 degrees. You can draw bunch of such triangles since length of any of the sides is not given. However, all these triangles are going to be congruent or similar to each other. Also, make sure the kids realize that the sides seem to have a fixed ratio to each other for a given angle. Make them find sine, cosine and tangent by measuring the lengths a, b, c and finding the ratios.
Ex: Repeat the exercise above with the other angle of the right angled triangle = 45 degrees. Again make the kid find out sine, cosine and tangent by measuring
Now, instead of drawing, let's try to find sine, cosine and tangent for special angles = 30, 45, 60. For angle=45, it's easy as the 2 sides are going to be the same (3rd side can be computed via pythagoras theorem), so ratios can be computed easily. For angle=30, we can make a reflection of the triangle, so that the 2 triangles combined become an equilateral triangle. Or we can draw an equilateral triangle and cut it in half. So, each half becomes a right angled triangle and the 2 halves are equivalent triangles, so, base is divided in half. Height can be found out by employing pythagoras theorem (h^2=a^2 - (a/2)^2 => h = √3/2*a.
For 0 degrees, the height of triangle is reduced to 0, so hypotenuse is equal to base. That gives us the values for 0. For 90 degrees, the base of triangle is reduced to 0, so hypotenuse is equal to height. That gives us the values for 90 degrees.
So, now we know to compute these for these important angles:
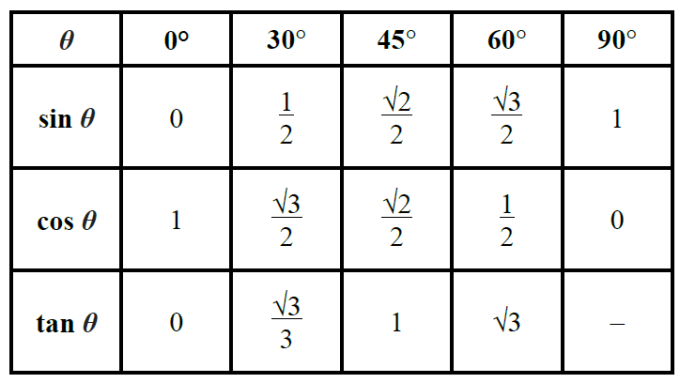
The easiest way to remember the basic values of sin and cos at the angles of 0°, 30°, 60°, 90°: sin([0, 30, 45, 60, 90]) = cos([90, 60, 45, 30, 0]) = sqrt([0, 1, 2, 3, 4]/4)
We can use the trignometric identities discussed earlier to get sin, cos, tan for 15 degrees and 75 degrees too.
- 15 degrees: Use Sin(A-B)=Sin(A).Cos(B)+Cos(A).Sin(B) => Sin(15)=Sin(45-30)=Sin(45).Cos(30)+Sin(30).Cos(45)=√2/2*√3/2+1/2*√2/2 = √2/4*(√3-1)
- 75 degrees: Use Sin(A+B)=Sin(A).Cos(B)+Cos(A).Sin(B) => Sin(75)=Sin(45+30)=Sin(45).Cos(30)+Sin(30).Cos(45)=√2/2*√3/2+1/2*√2/2 = √2/4*(√3+1)
There are trignometric tables provided which lists sin, cos, tan for all angles between 0 deg to 90 deg. These tables are very useful to find out sides or angles of a right triangle.


