- Details
-
Published: Monday, 07 September 2020 23:27
-
Hits: 1257
This is continuation of Elementary and Middle school maths. Here the topics are advanced. The STAAR question papers can be found for high school in the texas.gov website mentioned in Maths section.
Algebra:
We can move on to algebra 2 section for high school: https://www.mathsisfun.com/algebra/index-2.html
You may want to refresh Algebra 1 section from above website too (see in elementary maths section for details)
Functions:
Functions are a heart of algebra, as anything involving variables is a function. All real life processes are described in terms of functions, and then we solve them.
Khan Academy (Functions and Matrices): https://www.khanacademy.org/math/linear-algebra/matrix-transformations
Though some lessons from above are for Matrices, look at lessons on Functions, transformation, Inverse Functions.
A function is a relation where every domain (x) value maps to only one range (y) value. Strictly function is something that takes a set of values (called as range) and maps it to another set of values (called as range). NOTE: one "x" can have only one "y" and NOT more than one. As an ex: y=f(x)=x^2 always has only one y value for each x value. It's not possible that you plug in x=2 and you end up getting 2 y values. However, 2 x values can map to same y value, i.e both x=2 and x=-2 map to same y=4. So, y=x^2 is a function, but y=sq root(x) is not a function, as x=4 gives two y values, y=2 and y=-2. If we don't consider -ve values of sq root, then sq root becomes a function.
Inverse Function: Very important concept. A function f maps values from x to y. An inverse function [written as f-1(x) ] gets us from y back to x. Consider f(x)=x^2. Inverse function for this would be f-1(x)=√x. Let's choose x=2, then f(2)=4. Now if we apply inverse to 4, we should get 2. g(x)=√x. g(4)=2, So, g is an inverse function, i.e g(x)=f-1(x)=√x. F(x)=x is an identity function, as values remain same on transformation. It's inverse is also same, f-1(x)=x. Any given function has a unique inverse function, i.e it can't have more than one inverse function.
Mathematically f-1(f(x))=x and f(f-1(x))=x
In other way to visualize, functions are deviation from the line y=x, and inverse functions are deviations from that same straight line, but in opposite direction.
Power and Exponential Function:
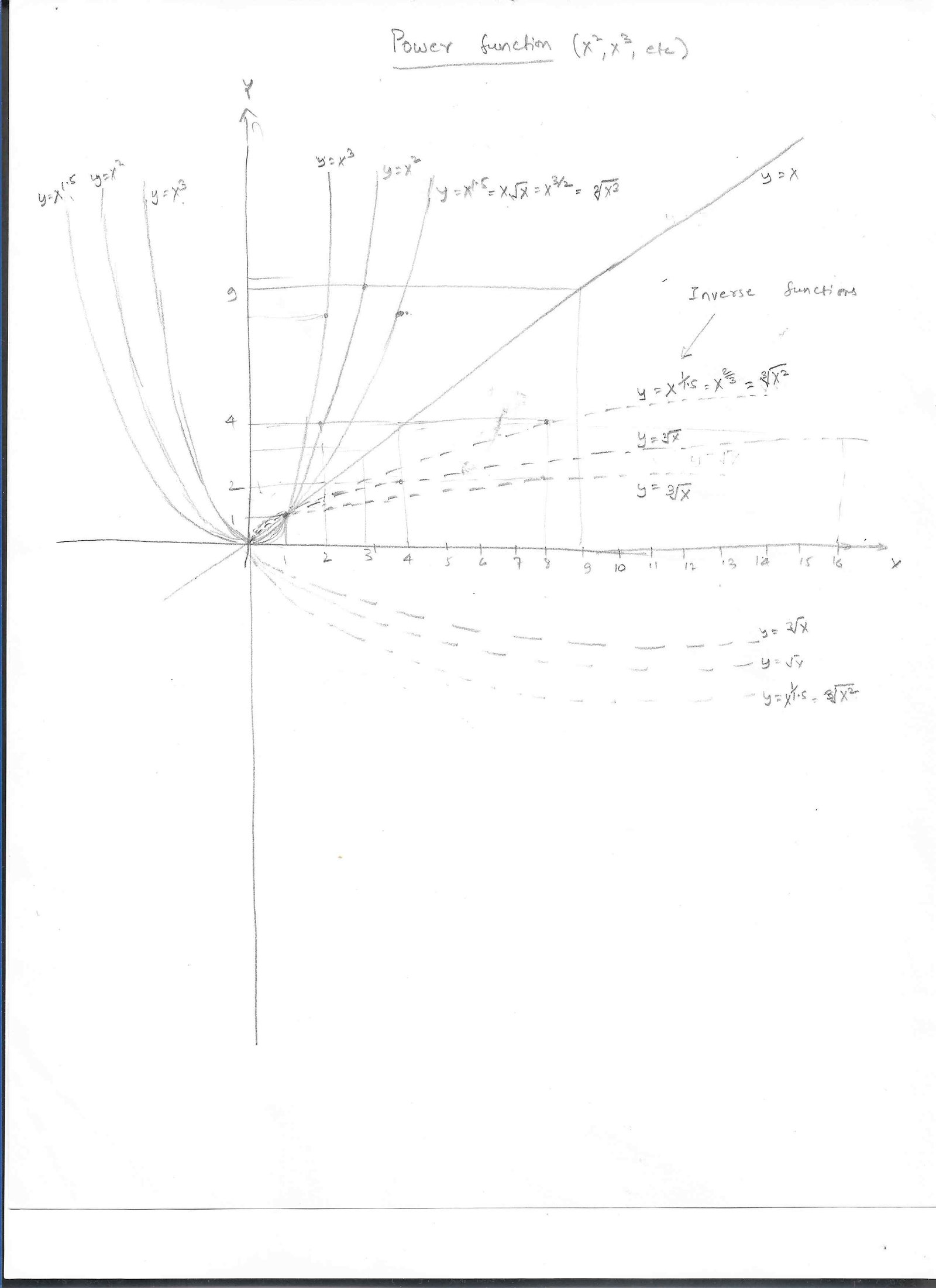
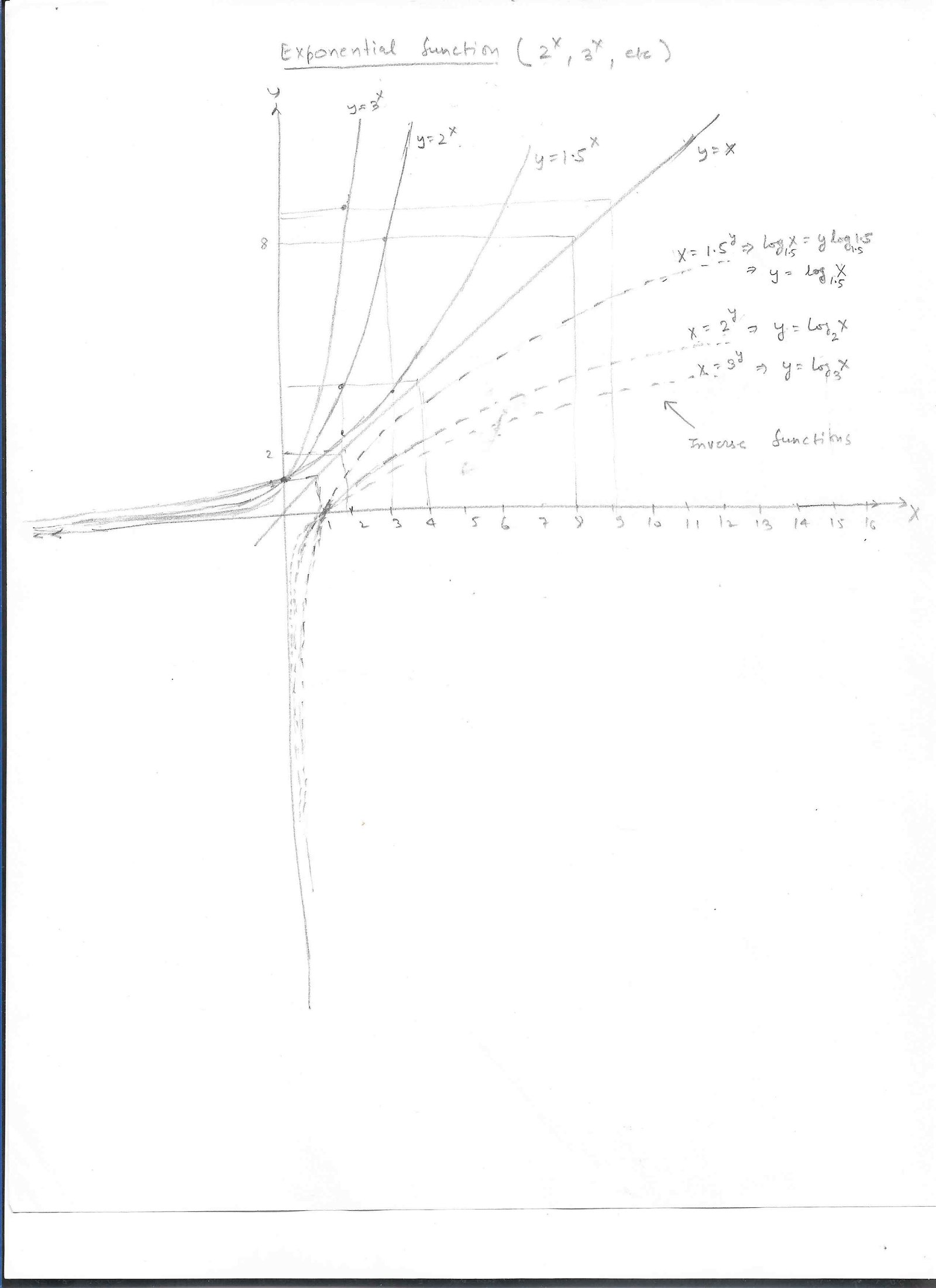
We looked at power functions (X^2, x^3) etc. Exponential func are 2^x, 3^x, etc. Exponential functions rise even faster than power functions as x appears in the exponent.
The plot below show the power function and it's inverse (which is sq root), and also exp func and it's inverse (which is log).
- Given f(x)=x^n, it's inverse is f-1(x)=x^(1/n). f-1(f(x))=f-1(x^n) = (x^n)^(1/n)=x^(n*1/n)=x^1=x. Also, doing the other way, f(f-1(x))= f(x^(1/n))=(x^(1/n))^n = x
- Given f(x)=a^x, it's inverse is f-1(x)= Logax (where "a" is the base of log). So, other way to look at log func is a^?=x. f-1(f(x))=f-1(a^x) = a^(Logax) = x.. Also, doing the other way, f(f-1(x))= f(Logax) = a^(Logax)= x
Plot of power function with inverse func:
Diagram showing power Func
Plot of exponential function with inverse func:
Diagram showing exponential Func
Log properties:
Link (with derivations) => https://www.cuemath.com/algebra/properties-of-logarithms/
NOTE: When base of log func is e, we call it natural log and write it as ln (w/o any base) instead of writing it as loge a which is same as writing ln a.
- logₐ mn = logₐ m + logₐ n (product property)
- logₐ m/n = logₐ m - logₐ n (quotient property)
- logₐ mn = n logₐ m (power property)
- logb a = (logc a) / (logc b) (change of base property) => Here we can change the log base to any new base "c".
From above properties, we can get many interesting properties:
- alogₐ x = x => This is very important property, that is used in a lot of log problems. This can be proved by taking log of both sides. Basically we are taking inverse of original function, so we get back "x".
- logbnam= (m/n)*logba. (It's b^n in base of LHS). This can also be proved by writing y=logbnam => y/m=logbna => b^(n*y/m)=a => n*y/m=logb a => y=(m/n)*logb a which is same as RHS
FIXME: upload hand drawn diagrams.
Polynomials:
We looked at algebraic expressions (i.e xy+2ab+4, etc) in the elementary maths section.
Each of xy, 2ab, 4 is a term. So, there are 3 terms in this expression above.
Terms are separated by +/-. anything separated by mult or div is not a term. If there is 1 term, it's called a monomial, 2 terms is called binomial, 3 terms is called trinomial, and so on. This whole family of terms is called polynomial. So, monomials are polynomials with only 1 term, binomial are poly with 2 terms and so on. NOTE: terms can only be counted once we have reduced the expression to a sum of product form with no parentheses remaining.
Degree of a poly: The greatest power or exponent of a polynomial is called its degree. So, x.y + a+5 has a degree 2, since it's first term has 1 power from x, and 1 power from y. Note that we add exponents within a term, even though the var are different and they can't be added. The reason we do that is because Degree of a poly refers to how fast the function is exponentially inc or dec. So, even if x and y are diff var, but func itself is moving at the rate of square (i.e if y is made same var as x, then it becomes x^2). Poly with degree of 2 is called Quadratic.
Polynomials are very important class of equations, and almost everything that is modeled in real life is expressed as polynomials. In fact, it has been proved that any complicated shape can be expressed as a polynomial. Each power of x has a constant multiplied with it called as "coefficient"
Addition/Subtraction: Polynomials can be added/subtracted. Only the terms with the same power of x can be reduced by adding/subtracting.
ex: 5x^2 + 2x + 7 + 9x^2+5x+5 = (5x^2+9x^2) + (2x+5x) + (7+5) = 14x^2 + 9x +12
Multiplication: Polynomials can be multiplied, by using the law of exponents explained in elementary maths section.
ex: (9x+5)*(7x^2+3x) = 9x*(7x^2+3) + 5(7x^2+3x) = 63x^3 + 27x + 35x^2 + 15x = 63x^3 + 35x^2 + 42x
Division: Division of polynomials looks tricky, but it can be done using same division method that we use for integer division. We find a multiplicand that can cancel out the term with the highest power of x. Then we move to the next highest power of x, and keep on doing so, until we are done, or left with a remainder.
ex: (2x^2+5x+7) / (x+5) => x+5 | (2x^2+5x+7) | 2x => x+5 | (2x^2+5x+7) | (2x-5) with remainder 32. We can check the answer by multiplying (x+5) and (2x-5). That gives: 2x^2+5x-25. If we add remainder of 32, then we get the original term: (2x^2+5x+7)
Other way to solve this is to divide the numerator in chunks of (x+5). i.e [ 2x(x+5) -5(x+5) +32 ] / (x+5) = 2x(x+5)/(x+5) -5(x+5)/(x+5) +32(x+5) = 2x - 5 + 32/(x+5)
ex: (3x^2+6x)/(x+2) =3x(x+2)/(x+2) = 3x
Plotting of Y vs X:
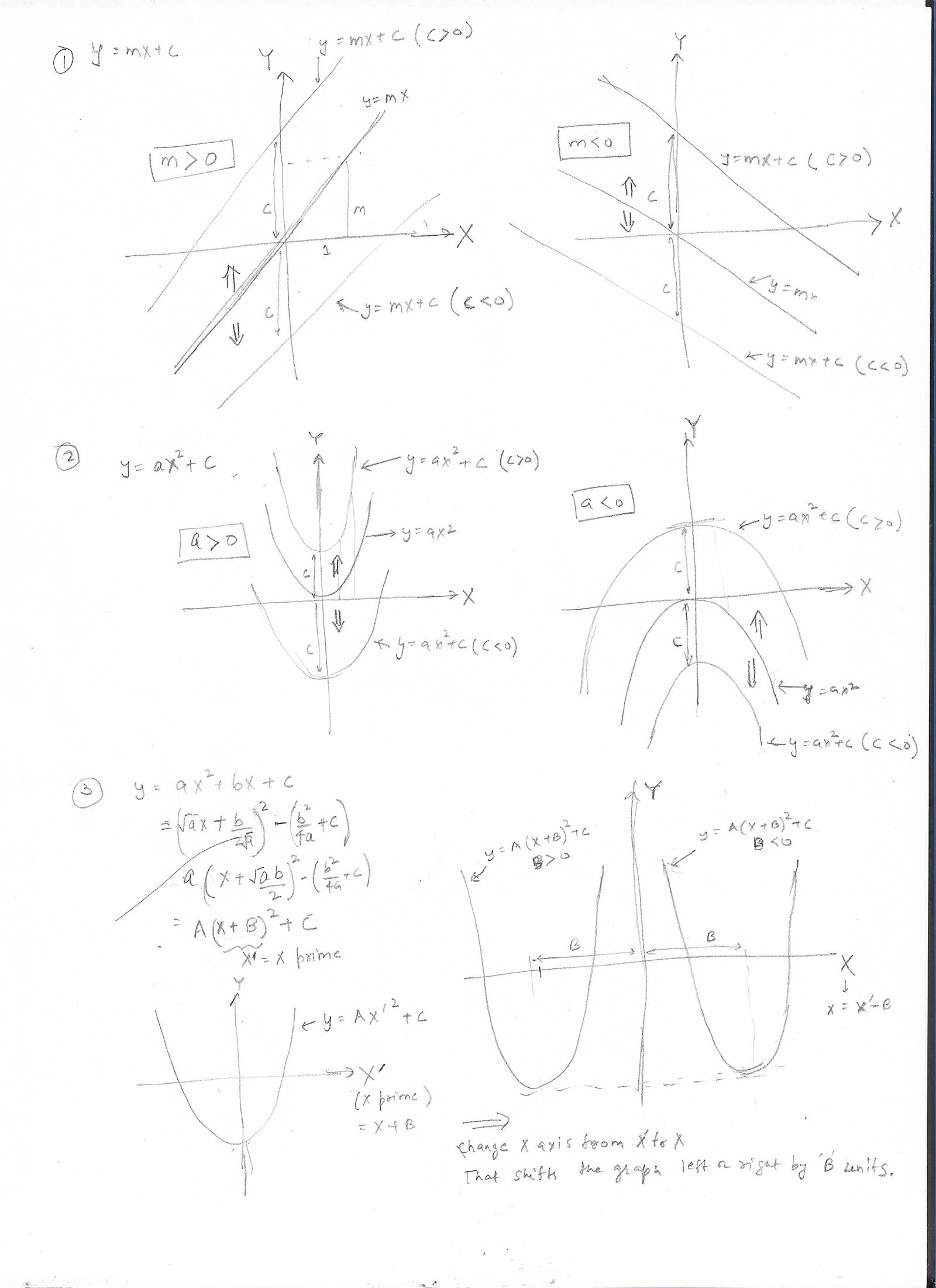
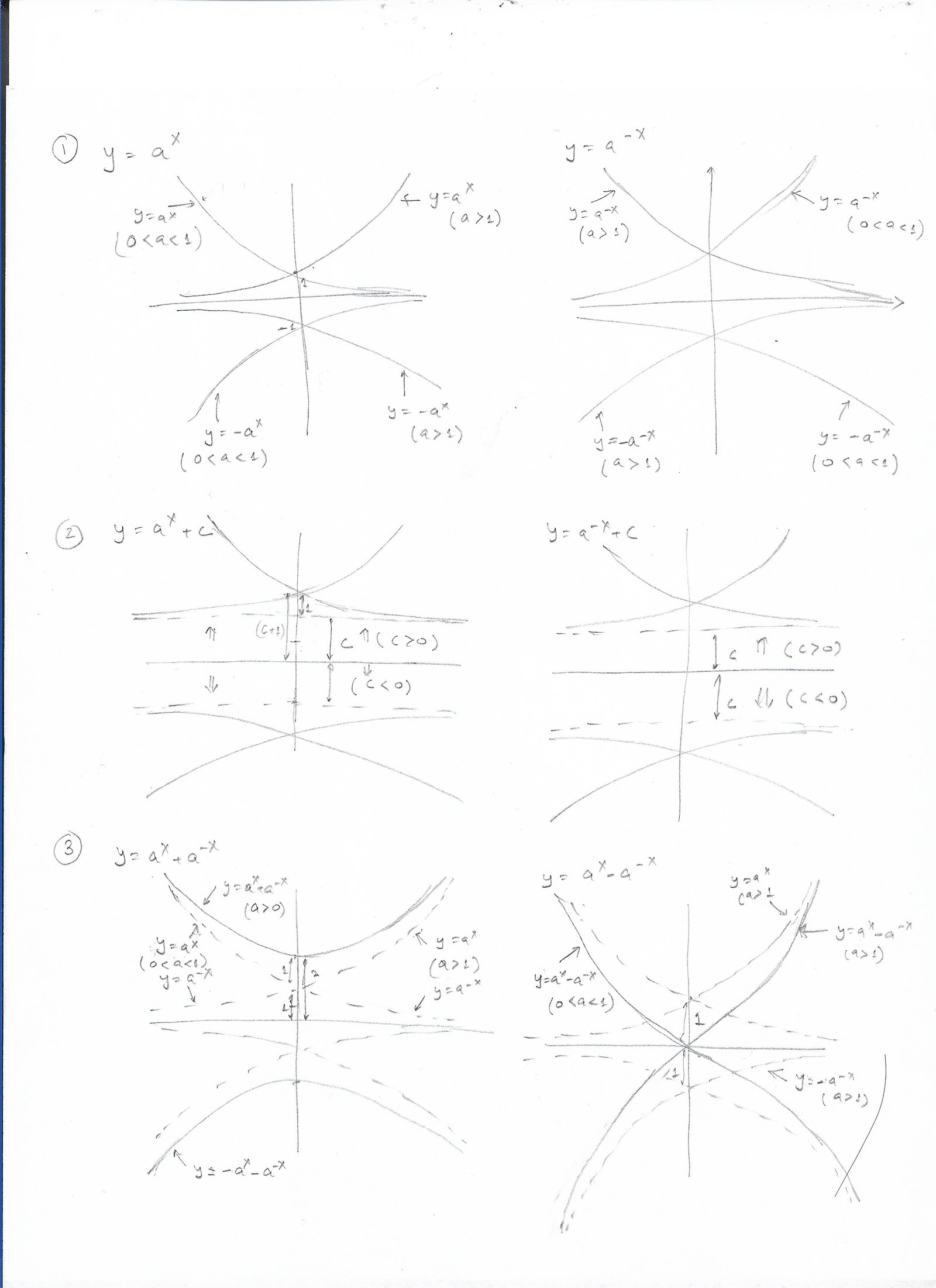
We looked at plotting of eqn of straight line in elementary school maths. High schools expands on that basic knowledge to plot more complicated shapes. We can plot polynomials too, though they are harder to plot. High school limits plotting polynomials to degree=2, which is quadratic equations. We also learn to plot exponential functions here. I've 2 plots below.
Plot 1: This details plotting straight line (linear function) and a curved u shaped line (quadratic function).
Plot of linear and quadratic functions
Plot 2: This details plotting simple exponential functions.
Plot of exponential functions
Algebraic Formula:
There are Formula for algebraic expression that help us in solving more complicated expressions by reducing or expanding them. Some common ones are:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a2 – b2 = (a – b)(a + b)
- (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
- a3 – b3 = (a – b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 – ab + b2)
Ex: To solve 57^2-43^2 => we can use identity a2 – b2 = (a – b)(a + b) => (57-43)(57+43)=6*100=600. If we try to solve it by taking squares, it will take lot longer.
Ex: To solve 57^2+43^2 => we can use identity (a + b)2 + (a - b)2 / 2 = (a2 + b2) => ( (57+43)^2 + (57-43)^2 ) /2 = 100^2 + 6^2 / 2 = 100036/2 = 500018
Binomial Theorem:
This is a generalization of (a+b)^n where n is any +ve integer n > 0.
Link: https://en.wikipedia.org/wiki/Binomial_theorem
Theorem was generalized by Newton to allow any real number n. Here (n r) is redefined as falling factorial, since factorial is only defined for integers. It was further generalized to allow complex numbers for x,y.
(x+y)n=∑k=0n(nk)xn−kyk=∑k=0n(nk)xkyn−k.{\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}=\sum _{k=0}^{n}{n \choose k}x^{k}y^{n-k}.}

Multinomial Theorem: The identity above is generalized to have more than 2 variables, and is called multinomial theorem.The general version (for +ve integer n > 0) is:
(x1+x2+⋯+xm)n=∑k1+k2+⋯+km=n(nk1,k2,…,km)x1k1x2k2⋯xmkm,{\displaystyle (x_{1}+x_{2}+\cdots +x_{m})^{n}=\sum _{k_{1}+k_{2}+\cdots +k_{m}=n}{\binom {n}{k_{1},k_{2},\ldots ,k_{m}}}x_{1}^{k_{1}}x_{2}^{k_{2}}\cdots x_{m}^{k_{m}},}

(1+x)n=∑k=0n(nk)xk,{\displaystyle (1+x)^{n}=\sum _{k=0}^{n}{n \choose k}x^{k}
Equations:
We looked at solving equations of 1 and 2 variables in the elementary maths section. We looked at linear equations there. Now we look at equations which are not linear in x and y, but have higher powers.
Equations of 1 variable:
Higher powers of x: Here x has higher powers to it. So, it's a polynomial in x. These equations don't have 1 solution for x, but multiple solutions. It has been proved that equation with powers of 2 (i.e x^2) have 2 solutions, x^3 have 3 solutions and so on. It has been proved that polynomial with power n, have n solution, which are called the n roots of the polynomial.
It's the Fundamental theorem of Algebra and applies to coefficients with complex coefficients too: https://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra
Finding n roots of any polynomial of degree n is not easy, but we know the relation b/w these n roots (roots may be real or imaginary, and may be repeated or unique) via Vieta's Formula: https://en.wikipedia.org/wiki/Vieta%27s_formulas
Complex numbers are explained in advanced Maths section.
We know how to solve x^2, but higher powers of x are harder to solve, and above formulae is used for solving it. Student is not expected to solve those, so we'll just concentrate on x^2 and x^3 (Degree of 2 and 3 are really popular questions in Maths olympiads).
Quadratic Polynomial (Power of 2): ex: x^2 + x = 5. This is called a quadratic equation. This can be solved via 2 ways:
1. Solving by using formula: It can be solved by using the formula for a*x^2 + b*x + c =0.Teach the kid how to derive that formula.
Derivation is not that hard: Look here: https://www.mathsisfun.com/algebra/quadratic-equation-derivation.html
An alternate way to solve is by using the same method as the derivation above. So, solve by making a square in form of (Ax+B)^2 -D + C = 0. Now bring numbers on RHS, take a square root, and solve for x.
ex: 2x^2+4x - 6 =0 => 2 (X^2 + 2x - 3) =0 => (x+1)^2 - 1 - 3 =0 => (X+1)^2 = 4 => (x+1) = +2,-2 => x=1,-3. So, this is exactly how quadratic eqn solution was derived above.
2. Other way to solve it is to bring it into the form a(x-p1)(x-p2)=0 where p1,p2 are the two solutions (or the 2 roots). There are 2 cases to consider.
- When coeff "a" = 1: Then x^2 - (p1+p2)*x + p1*p2 = 0. So, -b/a = the sum of the two roots = p1+p2, while c/a = product of 2 roots = p1*p2. This is a very important property used in factorizing the middle term. When p1,p2 are integers, then it's easier to find 2 such integers that will work. We can't rely on factorizing this if solution involve decimals. NOTE: IF the roots are p1 and p2, then the factors are -p1 and -p2. Since, -p1 + -p2 = b and (-p1)*(-p2)=c, for factorizing, we need to find 2 numbers such that their sum is b and product is c. Then the roots will be negative of those numbers, i.e if the factors are 2,3, then roots will be -2, -3. Important to remember this.
- ex: x^2 - 5x + 6 =0 => x^2-3x-2x+6=0 => x(x-3) - 2(x-3) =0 => (x-3)(x-2)=0 => 2 soln for this eqn: x=2 or x=3 (p1+p2=-5, p1*p2=6) => We are looking for 2 numbers whose sum is -5, but whose product is 6. One such pair of numbers is -2,-3. So, we get 2 factors as -2,-3.
- When coeff "a" ≠ 1: Above method of factorizing needs to be modified. We can always reduce such eqn to form where a=1 (by dividing whole quad eqn by a"), but then the coeff, b and c may become non integers, which is harder for humans to factorize. If roots are p1, p2, then a*[x^2 - (p1+p2)*x + p1*p2] = 0. Here a*(p1+p2)=-b, and a*p1*p2=c. So, the 2 roots p1, p2 satisfy p1+p2=-b/a and p1*p2=-c/a. What about the factors? Middle coeff "b" needs to separated into 2 terms -a*p1 and -a*p2 s.t (a*p1 + a*p2 = b), and (-(a*p1)*-(a*p2)=a*(a*p1*p2)=a*c). So, 2 factors are such that their sum is b, but their product is a*c. So, the 2 factors are -(a*p1) and -(a*p2), and the roots are p1, p2. Once factors are found, roots can be found by dividing the factors by -a.
- ex: 10*x^2-9*x+2=0 => Here we are looking for 2 numbers s.t their sum is -9 and their product is 10*2=20. 2 such numbers are -4 and -5. So factors of middle term are -5x, -4x => 10*x^2 - 5*x - 4*x + 2 =0 => 5*x(2x-1) - 2(2*x-1)=0 => (2*x-1)(5*x-2)=0 => The 2 roots are x=1/2, 2/5. This can also be solved for roots by dividing whole eqn by 10, and then looking for 2 numbers such that p1+p2=-9/10, p1*p2=2/10. One such pair is -4/10, -5/10. But it's much harder to see this as it's in fractions. So, we do it the other way suggested, as that keeps the 2 numbers as integers. The 2 roots can be found from the factors by dividing b -a=-10. So, 2 roots are -4/-10, -5/-10 = 2/5,1/2.
Solving for these eqn the other way round is lot easier. i.e eqn with form (x-2)(x-3) is lot easier to expand than solving eqn of form x^2 - 5x + 6 =0.
Cubic Polynomial (Power of 3): ex: x^3 + x^2 + x = 5. This is called a cubic equation. This is harder to solve. We can solve to by using Vieta's Formula to get relation among the 3 cubes which states:
For the 3 roots of a*x^3 + b*x^2 + c*x + d =0, p1+p2+p3 = -b/a, p1*p2 + p2*p3 + p1*p3 = c/a, p1*p2*p3 = -d/a.
Putting in the 3 roots => a*(x-p1)*(x-p2)*(x-p3)=0
Again, 2 ways to solve it, as in quadratic formula above. There are 2 cases to consider.
- When coeff "a" = 1: This is easy and same as quadratic case. Find 3 integers whose sum is -b, and product is -d. Those will be the roots. One way to solve it by guess, and see if you can get values for p1, p2, p3 (provided p1, p2, p3 are integers). Easy to find all possibilities of such integers, as there aren't too many combo possible.
- When coeff "a" ≠ 1: This gets harder. If roots are p1, p2, p3, then a*(x-p1)*(x-p2)*(x-p3)=0 => a*[x^3 - (p1+p2+p3)*x^2 + (...)x + p1*p2*p3] = 0. Here a*(p1+p2+p3)=-b, and a*p1*p2*p3=-d. Middle coeff "b" needs to separated into 3 terms -a*p1, -a*p2 and -a*p3 s.t -(a*p1 + a*p2 + a*p3 = b), and (-a*p1*-a*p2*-a*p3=-a*a*(a*p1*p2*p3)=a*a*d). So, 3 factors are such that their sum is b, but their product is a*a*d (NOTE the a^2 term here instead of 1 term in quadratic eqn). The factors are -a*p1, -a*p2, -a*p3, and then we can get thr roots by dividing the factors by -a.
- ex: 10*x^3 - 39*x^2 + 29*x - 6 = 0 (AMC 12 Maths Olympiad 2022). => Here we are looking for 3 numbers s.t their sum is -39 and their product is 10*10*-6=-600. Factorizing 600, we get 600=2^3*3*5^2. If we choose 3 factors as -30, -5, -4, then we see that we get 3 such numbers. So, 3 roots are obtained by dividing these factors by -a = 30/10, 5/10 and 4/10 = 3,1/2,2/5.
- There is another way to solve the above cubic poly. Expand x^2 coefficient and x coefficient into 2 components and then get 1 root. The other 2 roots will come from the quadratic eqn that we know how to solve. We ignore a for now, and assume a=1. Here we see that sum of these modified roots is 39, while product of these modified roots is 6. So, roots may be 1,1,6 or 2,3,1. We take 1 root as 3, then we break coeff 39 into 2 parts such that 1 factor is 3. If one part is 30, then we get 3 as a root => 10*x^3 - 30*x^2 - 9*x^2 + 27*x + 2*x - 6 =0 => 10*x^2(x-3) -9*x(x-3) + 2(x-3) =0 => (x-3)(10*x^2-9*x+2)=0. So 1 root is 3. The other 2 roots are from quadratic eqn 10*x^2-9*x+2=0, This has been solved above for roots=1/2, 2/5. This method works only because one the roots happened to be an integer. If all 3 roots were non integers, then this method won't work. It's a quick and dirty visual way to break components into factors.
Radical equation (power of 1/2 or square root, cube root, etc): ex: √(x+2) = 4. These are little tricky to solve. We solve them by converting them to quadratic eqn (for sq root) or to higher powers of x (for cube roots, etc)
One way to solve these is to square or cube both sides of eqn so that sq root, cube root,, etc are gone and we are left with just x, x^2, x^3 or so on, which we know how to solve.
ex: (x+2)^1/2 = 4 => sq both sides => (x+2) = 16 => x=14.
ex: (x+2)^1/2 = -4 => sq both sides => (x+2) = 16 => x=14. Here sq root of a number is set to -ve number. Strictly speaking, x=14 is a solution for this eqn too. However, for sq root eqn, we generally mean the +ve square root solution only. The -ve sq root solution is called extraneous soln, and is generally not considered correct. That's why we should plug in our answer, to see if we get the real soln or not. We need to throw away extraneous soln, and there is no way to know which soln is extraneous w/o plugging in our solved numbers back into the original eqn.
ex: √4 = +2,-2 => This has 2 soln (squaring 2 or -2, both yield 4). However, when we say sq root, we generally mean +ve sq root, so +2 is the real soln, and -2 is extraneous soln which is not considered correct.
NOTE: I'm guessing the reason we don't consider both +ve and -ve soln for √X is because √X won't be a function anymore, i.e for any value of X, we'll have 2 Y, which isn't a function.
Here's a link to solve radical eqn: https://www.mathsisfun.com/algebra/radical-equations-solving.html
Equations of 2 variable:
Higher powers of x and y: Here x and y have higher powers to them. These are even harder to solve, so calculus or computer programs are used to solve it. Depending on powers of x and y, they can have more than 1 solution.
ex: x^2 + y^2 = 13, x^3 + y = 19
Equations of more than 2 variables: Here we have n variables, as x, y, z. We can have linear or higher powers. These are also not expected to be solved by hand, except may be simple linear equation of 3 var = x, y, z.
ex: x+y+z=34, x+2y+z=38, 2x+y+z=44 => We can solve these 3 equations the same way we solve for 2 equations.
Series:
Arithmetic Series or Arithmetic Progression (AP): This is a series of number where each number differs from the next one by a constant number.
ex: 1, 5, 9, 13, ... => Here the difference between consecutive numbers is 4
finding sum of AP with n numbers, where a=1st number, and d=difference. i.e a, a+d, a+2d, a+3d, ... a+(n-1)d
Sum = a + (a+d) + (a+2d) + ....+ (a+(n-1)*d)
Sum = a + (a+(n-1)*d) + .... + (a+d)
=> 2*Sum = 2*a + (2*a+n*d)*(n-1)
=> 2*Sum = 2*a*n + n*d*(n-1)
=> Sum = n*[a + (n-1)*d/2]
ex: For simple AP series of S=1+2+3+...+N => Here a=1, d=1, n=N
=> S=N*[1+(N-1)/2] = N*(N+1)/2
Geometric series or Geometric Progression (GP): This is a series where the ratio between consecutive numbers is constant
ex: 1, 4, 16, 64, ... => Here the ratio between consecutive numbers is 4
finding sum of GP with n numbers, where a=1st number, and r=ratio i.e a, a*r, a*(r^2), a*r^3, ... a*(r^(n-1))
Sum = a + (a*r) + (a*r^2) + ....+ (a*r^(n-1))
r.Sum = (a*r) + (a*r^2) + ... + (a*r^(n-1)) + (a*r^n)
=> Sum - r.Sum = a - (a*r^n) => NOTE: all other terms cancel out
=> Sum(1-r) = a(1-r^n)
=> Sum = a(1-r^n) / (1-r)
ex: For simple GP series of S = 1 + 2 + 4 +8 + ... 2^N => Here a=1, r=2, n=N+1
=> S=1*(1-2^(N+1))/(1-2) = 2^(N+1)-1 => This summation is very useful in Binary number conversion to decimal in computer science
Sum of squares of first n numbers: This is proved by induction to be n(n+1)(2n+1)/6 (see in advanced math section for proof).
W/O induction it's hard. However a neat technique exists.
(n+1)^3 - 1^3 = 3n^3+3n^2+3n
Summation from i=1 to i=N for the expression Σ[(i+1)^3-i^3] will simply be (N+1)^3 - 1^3 as all terms in the series cancel out with each other (since we are subtracting the next number as well as adding the next number). => call it eqn (1)
However, if we simply expand (i+1)^3 into constituent terms, we can also write above expr as Σ[(i+1)^3-i^3] = Σi^3 + Σ3*(i^2) + Σ3*i + Σ1 - Σi^3 = 3Σ(i^2) + 3Σi + Σ1 = 3Σ(i^2) + N(N+1)/2 + N => call it eqn (2)
Eqn (1) and (2) are same. So, equating them, we get => (N+1)^3 - 1^3 = 3Σ(i^2) + N(N+1)/2 + N
=> N^3+3N^2 + 3N = 3Σ(i^2) + N(N+1)/2 + N
=> 3Σ(i^2) = N^3+3N^2 + 3N - N^2/2 - 3N/2
=> 3Σ(i^2) = N^3+3/2*N^2 + N/2
=> Σ(i^2) = 1/3*[N^3+3/2*N^2 + N/2] = N/6*(2N^2+3N+1) = N/6*[(N+1)(2N+1)] => which is the same formula as above
Sum of cubes of first n numbers: This is proved by induction to be [n(n+1)/2]^2 (see in advanced math section for proof). It's just square of sum of 1st n numbers.
To find the formula itself for cubes, we can use the same technique as above. Little longer, but nothing different.
Sum of ith power of first n numbers:There is a general formula involving Bernoulli's numbers and coefficients. Ask ChatGPT for formula.
Simple and Compound Interest:
This is a topic that is introduced in Elementary maths, but I included it here, since compund interest requires solving eqn with higher powers of X.
Simple Interest: Introduce the concept of principal and interest when money is deposited in a bank. Introduce the concept of rate per annum, as well as per quarter, per month, or rate per day. It should be clear that all these rates mean different effective rate.
SI for T years = P*(R/100)*T => Where P=principal, R=rate in % p.a, T=total time in years
Total Principal after T years = P *( 1+R*T/100)
Compound Interest: Compound interest is the compunded interest, where you get interest on the interest too. This seems more fair, since if the bank didn't give you interest on your earned interest, then you scould withdraw that interest, put that interest amount in other bank, and start earning earning interest on that.
CI for 1st year is same as SI for 1st year, if interest rate is per annum
CI (for 1st year) = P*(R/100)
A1 = Total Principal after 1 year = P *( 1+R/100)
CI (for 2nd year) = A1*(R/100)
A2 = Total Principal after 2 years = A1+ A1*R/100 = A1*(1+R/100)
CI (for 3rd year) = A2*(R/100)
A3 = Total Principal after 3 years = A2+ A2*R/100 = A2*(1+R/100) = A1*(1+R/100)^2 = P*(1+R/100)^3
Similarly AT = Total Principal after T years = P*(1+R/100)^T
So, Total Principal after T years = P *( 1+R/100)^T
Conclusion: As can be seen above, CI is more than SI for any year after the 1st year, and total Principal with compound interest is lot more than that with simple interest.
Matrix:
Matrix is one the simple topics, but rather important one to learn. The usage of matrix is not apparent, as it's just a way of representing numbers. Matrices are widely used in computer programming to rep a large set of numbers, and operate on them efficiently.
Good material here: https://www.mathsisfun.com/algebra/matrix-introduction.html
Various operations of +, -, *, / are explained on link above. Most interesting is the multiplication of 2 matrices which is known as the "dot product" of 2 matrices. Most important thing to remember about matrix multiplication is that:
To multiply an m×n matrix by an n×p matrix, the ns must be the same, and the result is an m×p matrix.
i.e (mXn) dot (nXp) = (mXp) matrix
So ... multiplying a 1×3 by a 3×1 gets a 1×1 result. But multiplying a 3×1 by a 1×3 gets a 3×3 result.
NOTE: Terms "Multiplication of 2 matrices" and "Dot product of 2 matrices" are used interchangeably. It's OK to use them with the understanding that multiplication is actually dot product. Multiplication of a matrix with a scalar is simply multiplying each entry of the matrix with that scalar. So, be careful when you see these terms.
Advanced:
Advanced maths topics on Limits, calculus, etc are in next section. I'll start that section in some time. Note that if you are preparing for SAT exam, then everything until is point is all you need. SAT Maths don't need you to know any advanced stuff about calculus, etc. Basic linear and quadratic equation solution, and basic High school maths can easily fetch you 100% score in SAT Maths.







